Deconstructing Sound: The Harmonic Series
If a tree falls in a forest and nobody is around to hear it, does it make a sound? This old question doesn't really cause most people to stop and ponder anymore, mainly because the solution isn't that interesting. The answer being: It depends... Do we define sound as the subjective experience of hearing vibrations in the air? Or do we define sound as the actual vibrations in the air, regardless of whether or not those vibrations reached any ears? For the purposes of this post, we will use the latter, objective definition of sound. So why do these vibrations in the air occur, and how do they produce such a wide variety of sonic experiences?
Figure 1
Imagine a top down 2-D floorplan of the room you are sitting in. Now imagine that the shape of that floorplan is the shape of a pond that you are standing next to. Toss a pebble into that pond. This pebble represents a single sound that was made in the room, like clapping once for instance. When the pebble hits the water, it causes ripples on the surface that expand radially in all directions. Those ripples will travel outwards in concentric circles until they hit the edge of the pond, in which case they will bounce off in the opposite direction. Eventually the ripples will dissipate.
This pond analogy shows how sound waves will travel outwards in all directions from the source, losing energy as they go and as they bounce off of walls. The only difference is that in real life sound travels in three dimensions and the waves propagate much faster, 767mph at room temperature, fast enough to bounce between walls in the room hundreds of times in a second. The waves that travel directly from the source to your ears is the main sound you hear, while the waves that bounce off the walls and come back to your ears a split second later are the reverberations.
Because the waves are moving in three dimensions rather than over a two dimensional surface like in a pond, sound waves will "wave" a bit differently than water waves. Rather than moving vertically up and down as waves along the surface of water, sound waves are compression waves (or longitudinal waves), which wave in the direction of travel. You can think of it as like a spring that compresses and stretches as it travels along. The air is being squeezed together and then stretched out, over and over, hundreds or thousands of times a second. The faster it squeezes and stretches, the higher the pitch of the sound.
Figure 2
The other properties of sound are frequency and wavelength. Frequency is how many waves happen in once second. More specifically, how many cycles of peak to valley and back to peak again occur in one second. The faster the waving, the higher the pitch of the sound. The units we use to measure frequency are Hertz (Hz), with 1 Hz meaning one cycle per second. A sound at 440Hz is cycling at 440 times per second. Wavelength is a bit more complicated and isn't necessary to know before we move on, but it means the physical length in space one cycle takes up (e.g. 440hz has a wavelength of approx. 78cm) and can be derived from the frequency and the speed of sound.
Now that we have covered the basics of sound waves, let's see how they make up the sounds we hear every day. We know that sound waves at different frequencies produce different pitches, but how come when two instruments (or two singers) play the same note, they still sound very different?
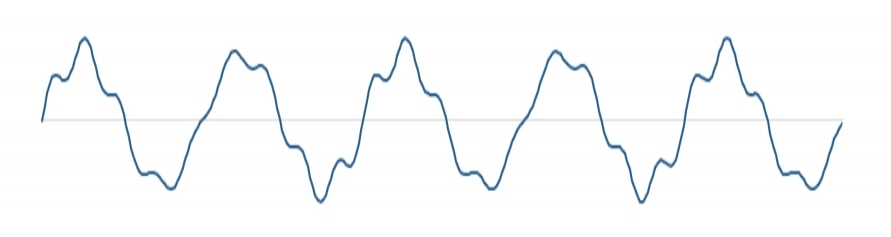
A simple, smooth wave like in fig. 2 is called a sine wave, and produces a very pure, uninteresting beep. Most of the pitched sounds we hear in real life are complex sounds which have jagged, seemingly-irregular waves, like in fig. 3.
Figure 3
The wave looks chaotic, but it is actually made up of several different sine waves stacked on top of each other. When two different waves occupy the same space, the peaks will reinforce each other while the valleys do the same in the opposite direction. When a peak and a valley meet, they cancel each other out and no sound is produced. Through some very complex math (the Fourier transform) we can extract all the different sine waves that make up a complex sound (fig. 4).
Figure 4
Figure 5
Figure 6
The singer's formant is a clustering of harmonics produced by the human voice between 2.5k and 3.5kHz.
More on that in the next post.
Notice in the frequency graph in fig. 6, the different harmonics are represented as bold lines stacked on top of each other, but some are bolder (louder) than others. The relative loudness or softness of one harmonic versus another determines the tone quality. That is, the ratio of the perceived loudness of each harmonic makes up the unique tonal fingerprint of each sound. That is why a piano will sound different than a clarinet will sound different than the voice, even if they are all playing the same note! One of the main reasons they sound different is because a piano has louder second and fourth harmonics and a clarinet has comparatively very quiet second and fourth harmonics (fig. 7).
Figure 7
The voice on the other hand, can change the relative loudness of the different harmonics to make different sounds. That is what our mouth is doing when we sing through different vowels. Each vowel makes a unique harmonic fingerprint, just as each instrument does. The harmonic series provides an infinite variety of possible tone colors for each and every note, and we as singers change our tone color wildly as a part of making language.
The next post in this series on the nature of sound will cover how we manipulate the harmonics in our voice with our mouth and tongue as we shape different vowels. We will learn about formants, why some vowels are easy to sing in certain parts of our range while others need to be adjusted, and how we can project our voices without the aid of a microphone. See you next time!
~Alexander
1 - Other factors like resonance and frequency distribution can affect the perceived loudness
2 - Fo stands for for Fundamental Oscillation. Note the letter O and not the number 0. The notation 3Fo is for calculating the frequency of the harmonic: e.g. if the fundamental Fo = 440Hz then 3Fo = 3 * 440Hz = 1320Hz.